32 ORE AL GIORNO

 

Dite la verità: quante volte vi siete trovati nella situazione di non riuscire a fare tutto ciò che avevate in programma di fare?

E quante volte avete pensato che 24 ore al giorno fossero poche e che ne servissero di più?

Beh, io ve ne prometto 32!

Come? Ma è facilissimo: rallentando la rotazione della terra...

 

di Lola Fox

 

 

 

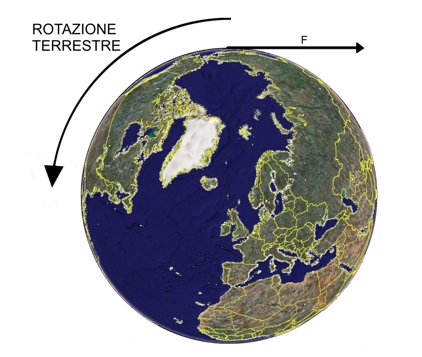
Ancor prima che tu, caro lettore intelligente e curioso ma anche tremendamente perditempo, possa pensare che io sia pazzo, ti comunico che stai consumando pensieri, quindi energie per nulla, in quanto sono il primo io a dichiararmi pazzo. Bene. Dopo questa premessa dovuta (uh, una cosuccia da nulla, cosa vuoi che sia essere pazzi, c'è chi sta peggio: i matti...) che vanifica ogni tuo ulteriore pensare al riguardo, passiamo seriamente alla follia. Questo progetto, sulla carta non fa una piega, esattamente come non faceva (quasi) una piega quell'idea di quel tizio che nel 1978 andò a Portobello da Tortora a proporgli di spianare il passo del Turchino per eliminare la nebbia in val Padana. Dopotutto io propongo solo di applicare una forza F contraria al senso di rotazione terrestre, atta a rallentarla, come illustrato in figura 1: una robetta da nulla, cosa vuoi che sia?

 

Avete presente quelle ruote giranti durante gli spettacoli pirotecnici? Mettono una fontana pirotecnica, un piccolo razzetto che fà le fiammelle colorate,

Fig. 1

attaccato ad una ruota, ed essa, all'accensione del piccolo razzo, inizierà a girare. Ecco l'idea: se noi mettiamo un grande razzo ancorato alla terra, e lo accendiamo in senso contrario alla rotazione, la sua forza rallenterà la rotazione terrestre ed io avrò il giorno di 32 ore. Bene, questo è proprio ciò che voglio ottenere: rallentare la rotazione della Terra applicandogli una forza contraria.

 

Già ma che forza? Da dove parto? É molto semplice: dagli unici dati che disponiamo e da quelli che vogliamo ottenere. Siccome per spendere meno energie applicherò la mia contro-forza sull'equatore dove il raggio dall'asse di rotazione, è maggiore, andrò a segnarmi il primo dato:

 

- RAGGIO TERRESTRE ALL'EQUATORE (r): 6.378,14 km (6,38*10⁶ m)

 

Dice: ma se tu vai in cima all'Everest, guadagni ulteriori 9 Km no? Nain! L'Everest si trova a circa 28° Nord di latitudine dove il raggio, dall'asse di rotazione, è pari a cos28 * 6.378,14 Km = 5.631,56 Km a cui aggiungiamo 9 km di Everest, per cui lassù sei solo a 5.640 Km dall'asse di rotazione. Troppo pochi.

Ri-dice: beh, allora vai sul Kilimanjaro che sei in pratica sull'equatore ma almeno guadagni 5-6 km. Il Kilimanjaro è a 3° S di latitudine per cui il raggio è: cos3 * 6.378.14 Km = 6.369,40 m ma siccome la sua cima è a quota 5,89 km il totale diventa 6.375 km: per 3 km non ce la facciamo!

 

A che velocità ruota un oggetto posto sull'equatore rispetto ad un osservatore esterno e fermo rispetto alla Terra? Il conto è presto fatto: se in 24 h la terra fa un giro completo, cioè 360° (che sono 2¶ radianti, cioè 6.28 rad), la mia velocità angolare (detta w) sarà 6.28/24 = 0.2617 rad/h che moltiplicato per il raggio terrestre, dà una velocità sull'equatore (detta v1) di circa 1.669.16 Km/h.

Ma io voglio avere 32 ore al giorno, quindi rallentando la rotazione terrestre, anche la velocità periferica scenderà a 6.28/32 = 0.1962 rad/h che moltiplicato x il raggio terrestre dà una velocità periferica (v2) di 1.251.71 Km/h. Riassumendo quindi

 

 

- VELOCITÀ PERIFERICA ALL'EQUATORE (v1) : 1.669,16 Km/h - 463.66 m/sec

- VELOCITÀ PERIFERICA ALL'EQUATORE (v2) : 1.251,16 Km/h - 347.50 m/sec

 

Quindi io dovrò portare questa velocità da 1.66,16 Km/h a 1.251,16 Km/h con una variazione negativa di velocità (che chiameremo  ∆v) di 418 Km/h pari ad una differenza di velocità angolare di 418/6.378,14 = 65,54*10^-3 rad/h

 

-DIFFERENZA DI VELOCITÀ PERIFERICA (∆v) : 418 Km/h - 116.11 m/sec)

-DIFFERENZA DI VELOCITÀ ANGOLARE (∆w) :  65,54*10^-3 rad/h

 

Ora devo stabilire un tempo ragionevole affinché la mia forza rallentatrice compia il suo dovere. Devo però considerare che l'impresa è titanica per cui mi prendo 1 anno, cioè 365 giorni, cioè 8.760 ore cioè 31,536*10⁶ sec di applicazione continua della mia forza rallentatrice.

 

- TEMPO DI DECELERAZIONE (t) : 1 ANNO = 31,536*10⁶ sec

 

Avendo una velocità di 418 km/h da perdere in un anno, avrò una decelerazione di 418 km/h diviso 8.760 ore che fa 0.048 km/h² cioè ogni ora che passa, la mia velocità rallenterà di 47 m/h . Una decelerazione praticamente inavvertibile, che non farà manco crepare il vetro di un grattacielo: nessuno se ne accorgerà. Vi va molto peggio quando sull'autobus l'autista frena di colpo, fermando in 2 secondi il mezzo che viaggiava a 30 km/h, perché in questo caso ricevete una decelerazione di 30 km/h ovvero 8.33 m/sec diviso 2 sec fa 4.165 m/sec² . Questo dato, che corrisponde +/- a metà dell'accelerazione di gravità "g" è oltre 1 milione di volte superiore a quella che vi darò io.

 

La Terra ha una massa che è circa 5.967.522.543.000.000.000.000 ton (ho rotto parecchie bilance prima di pesarla correttamente) cioè 5.967 miliardi di miliardi di ton che abbreviando in Kg, ottenendo

 

- MASSA DELLA TERRA (m) : 5,968*10²⁴ Kg

 

Essendo un corpo in rotazione, considerato +/- sferico e +/- omogeneo, ci serve il suo momento d'inerzia dato dalla relazione 2/5*m*r² cioè 2/5 * 5,968*10²⁴ Kg * (6,38*10⁶)² m = 97,17*10³⁶ Kgm²

 

- MOMENTO D'INERZIA (I) : 97,17*10³⁶ Kgm²

 

Ora dobbiamo sapere quanta quantità di moto serve, ovvero quale sarà la differenza del momento angolare tra la rotazione originale a quella rallentata: questo si ottiene tramite il prodotto del sopracitato momento d'inerzia I per la differenza di velocità angolare ∆w, ovvero 97,17*10³⁶ Kgm² * 65,54*10^-3 rad/h = 63,69*10³⁴ Kgm²/h che sarebbero 17,69*10³¹ Kgm²/sec

 

- VARIAZIONE DEL MOMENTO ANGOLARE (∆L) (QUANTITÀ DI MOTO NECESSARIA) : 17,69*10³¹ Kgm²/sec

 

 

Orbene, ci siamo! Adesso sapremo finalmente quanta forza dovrà avere il nostro super razzo per dare questa quantità di moto alla Terra dall'equatore. La formula è semplice: la quantità di moto diviso il tempo per il quale dovremo tenere acceso il nostro razzo (1 anno cioè 31,536*10⁶ sec) ci darà il momento meccanico che serve a rallentare la terra: 17,69*10³¹ Kgm²/sec / 31,536*10⁶ sec = 360,95*10²² Kgm²/sec² cioè Nm. Che diviso per il raggio della nostra Terra fa: 360,95*10²² Nm / 6,38*10⁶ m = 56,58*10¹⁶ N

 

- FORZA NECESSARIA (F) : 56,58*10¹⁶ N

 

Bene ! Serve un razzo da 565 miliardi di MN. Uhmmm.... Sento uno strado odore... Una certa aria...

Mi sovviene che il mitico Saturno V che spinse 12 uomini verso la Luna aveva 33 MN per cui... ehm... se io... s-si... cioè... in pratica... ehmm... se... no... si... cioè... ne prendo... ehmm... 17 o 18 miliardi (di razzi Saturno V) e li tengo accesi per un anno, riesco ad avere 32 ore in giorno.

 

Sento...

 

Sento...

 

Sento che mi stai mandando a fare in culo... :-)

 

 

 

(Si ma, confessa, ti è piaciuto)